Artificial Intelligence - Heuristic/Local search

Heuristic Function
• A heuristic function h(n) yields the estimated cost of the cheapest path from the state at node n to a goal state.
• What do we mean by “heuristic”?
- Oxford Dictionary: Proceeding to a solution by trial and error or by rules that are only loosely defined.
- Wikipedia: A technique designed to solve a problem that ignores whether the solution can be proven to be correct, but which usually produces a good solution or solves a simpler problem that contains or intersects with the solution of the more complex problem.
- In this post - ex) Greedy Best-First Search and A*
Search Terminology

- Tree Search
1 2 3 4 5 6 7 8 9 10 | frontier.add(INITIAL_STATE) while not is_empty(frontier): node = frontier.get_next_node() for nd in expand(node): if is_goal(nd): return solution elif (nd not in frontier): frontier.add(nd) return failure | cs |
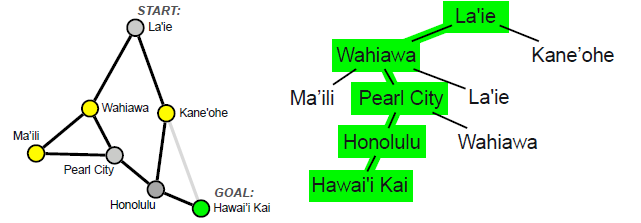
- Graph Search
1 2 3 4 5 6 7 8 9 10 11 12 | frontier.add(INITIAL_STATE) explored = {} while not is_empty(frontier): node = frontier.get_next_node() explored.add(node) for nd in expand(node): if is_goal(nd): return solution elif (nd not in frontier) and (nd not in explored): frontier.add(nd) return failure | cs |
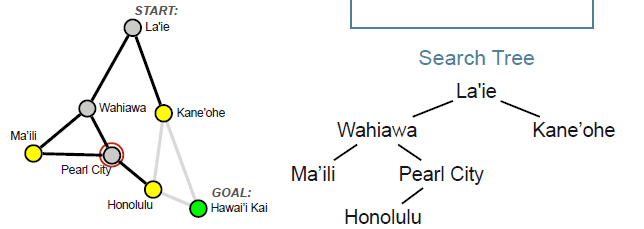
-
Tree Search vs. Graph Search
- Without some sort of bookkeeping, naive tree search methods may repeat themselves, possibly ad infinitum
- Graph search methods maintain a data structure to track previously explored states, avoiding repetition
- Graph search is going to take up more space given the extra data structure
- For our purposes, we’ll always assume that we’re using graph search unless explicitly said otherwise
- Breadth-First Search (BFS)
1 2 3 4 5 6 7 8 9 10 11 12 | frontier.add(INITIAL_STATE) # FIFO queue explored = {} while not is_empty(frontier): node = frontier.pop() # dequeue explored.add(node) for nd in expand(node): if is_goal(nd): return solution elif (nd not in frontier) and (nd not in explored): frontier.add(nd) return failure | cs |
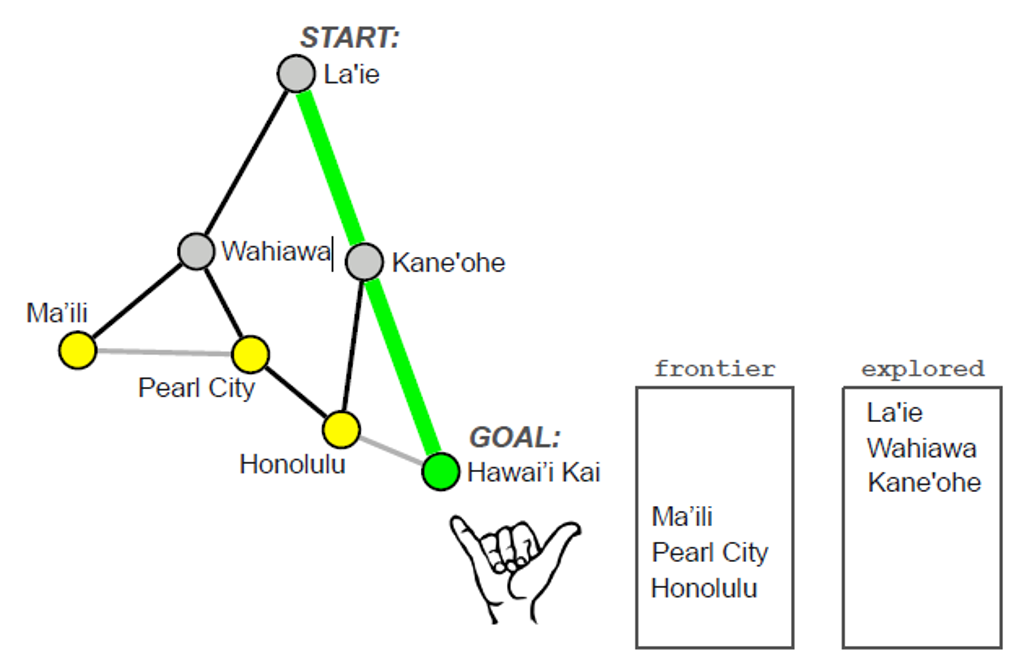
- Complete? Yes (if branching factor b is finite)
- Optimal? Yes, if step costs are identical, but not in general
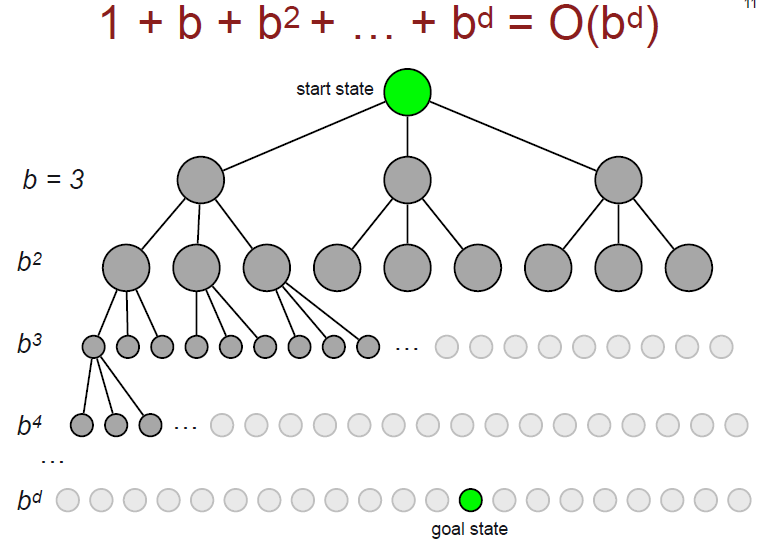
- Time? 1+b+b2+b3+…+bd = O(bd)
- Space? O(bd) (b = branching factor, d = depth of solution)
- Depth-First Search (DFS)
1 2 3 4 5 6 7 8 9 10 11 12 | frontier.add(INITIAL_STATE) # LIFO stack explored = {} while not is_empty(frontier): node = frontier.pop() explored.add(node) for nd in expand(node): if is_goal(nd): return solution elif (nd not in frontier) and (nd not in explored): frontier.add(nd) return failure | cs |
DFS ( Graph )
1 2 3 4 5 6 7 8 9 10 11 12 13 | frontier.add(INITIAL_STATE) # LIFO stack explored = {} while not is_empty(frontier): node = frontier.pop() explored.add(node) for n in expand(node): if (n not in frontier) and (n not in explored): if is_goal(n): return solution else: frontier.add(n) return failure | cs |
DFS ( Tree )
1 2 3 4 5 6 7 8 9 10 11 12 13 | frontier.add(INITIAL_STATE) explored = {} while not is_empty(frontier): node = frontier.pop() for n in expand(node): if (n not in frontier): if is_goal(n): return solution else: frontier.add(n) return failure | cs |

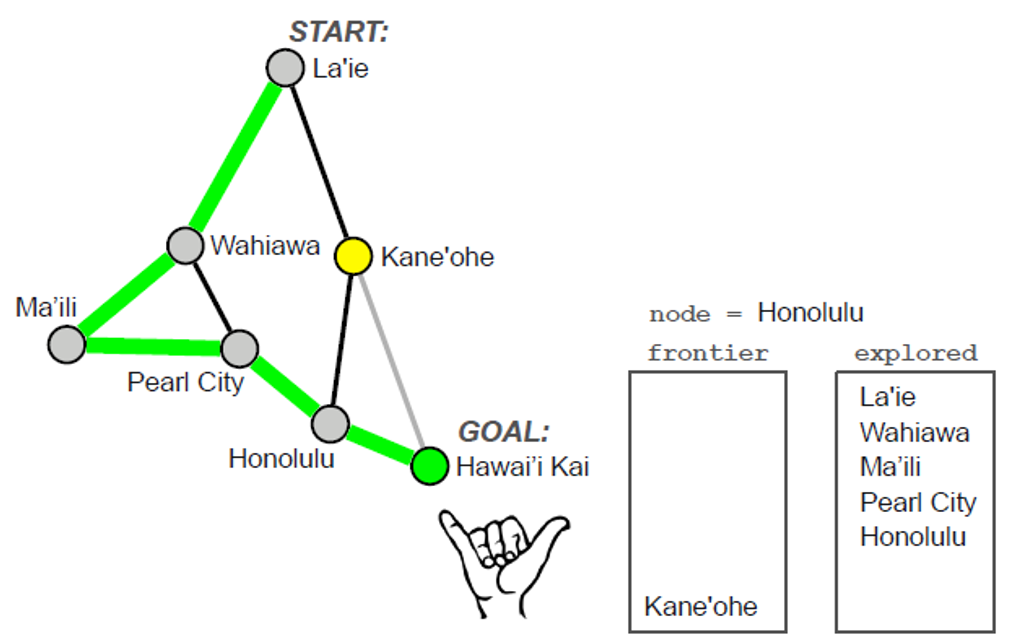
- Uniform-Cost Search
• How can we modify BFS to retain optimality in problems with different transition costs?
• Intuition: expand nodes in order of least path cost so far
• Instead of FIFO or LIFO queue, store frontier as a priority queue
• Recall: priority queues are an abstract data type that holds a collection of elements associated with a (usually numeric) priority, such that higher priority items are dequeued (popped) before lower ones.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | frontier.add(INITIAL_STATE) # Priority queue explored = {} while not is_empty(frontier): node = frontier.pop() if is_goal(node): return solution explored.add(node) for nd in expand(node): if (nd not in frontier) and (nd not in explored): frontier.add(nd) else if (nd in frontier) and (frontier.get(nd) > nd.cost): frontier.update(nd, nd.cost) return failure | cs |
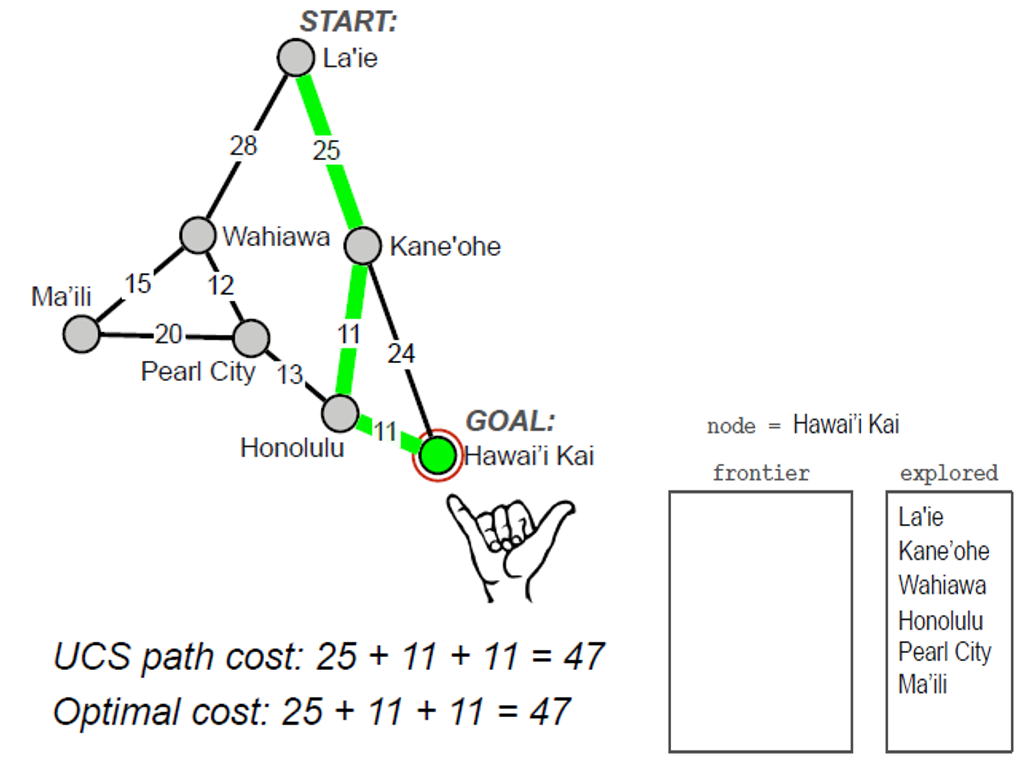
- Complete? Yes
- Optimal? Yes
- Time? O(b^(1+[C*/ϵ]))
- Space? O(b^(1+[C*/ϵ]))
(b = branching factor, C* = cost of optimal solution, ϵ = minimum step cost)
- Greedy Best-First Search
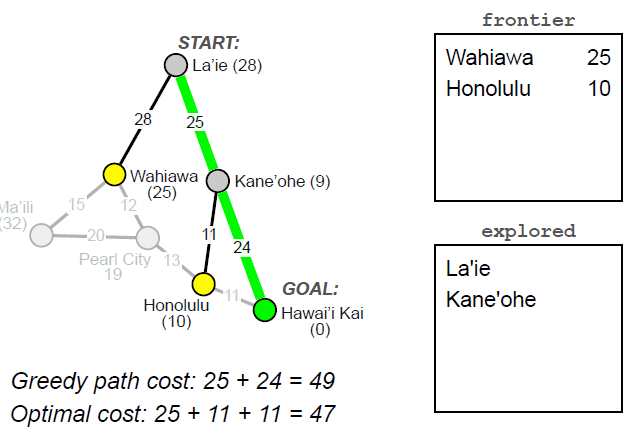

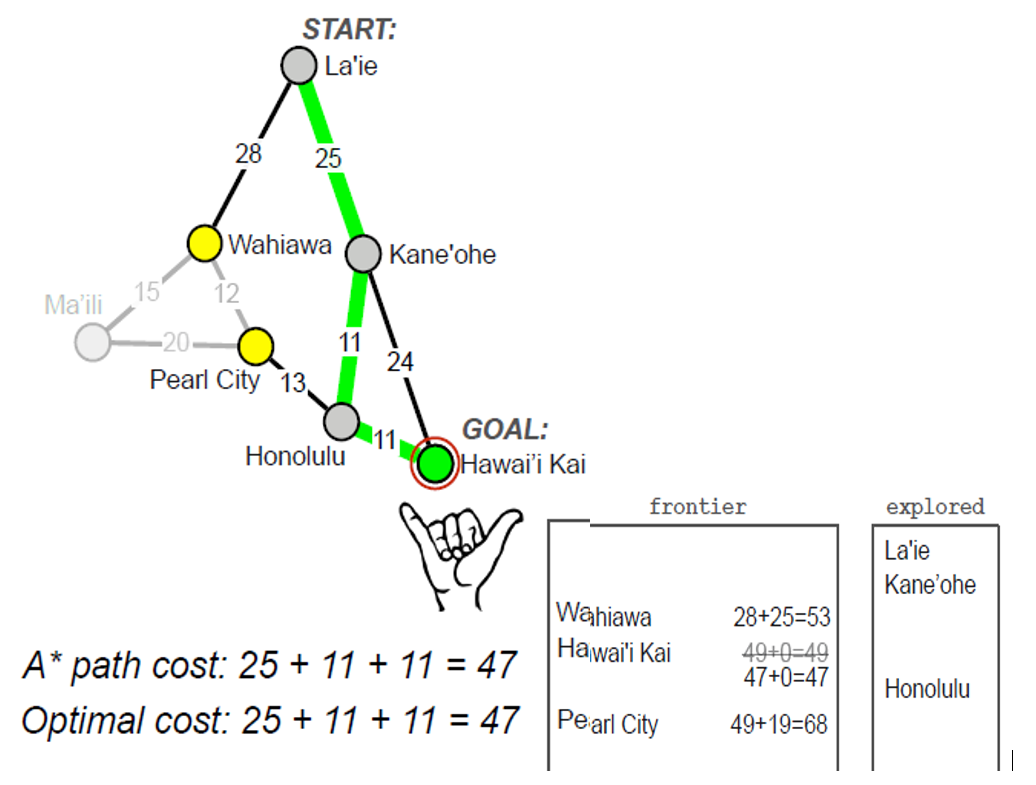
- A* Search
- Intuition: avoid expanding paths that are already expensive, but still prefer those that seem closest to the goal
- Evaluation function:
- f(n) = g(n) + h(n)
- g(n) = cost so far to reach state n (like UCS)
- h(n) = est. cost of cheapest path from n to goal (like Greedy)
- f(n) = est. cost of cheapest path through n to goal
1 2 3 4 5 6 7 8 9 10 11 12 13 14 | frontier.add(START_STATE, 0) explored = {} while not is_empty(frontier): node = frontier.pop() if is_goal(node): return solution explored.add(node) for nd in expand(node): if (nd not in frontier) and (nd not in explored): frontier.add(nd) else if (nd in frontier) and (frontier.get(nd) > nd.cost): frontier.update(nd, nd.cost) return failure | cs |

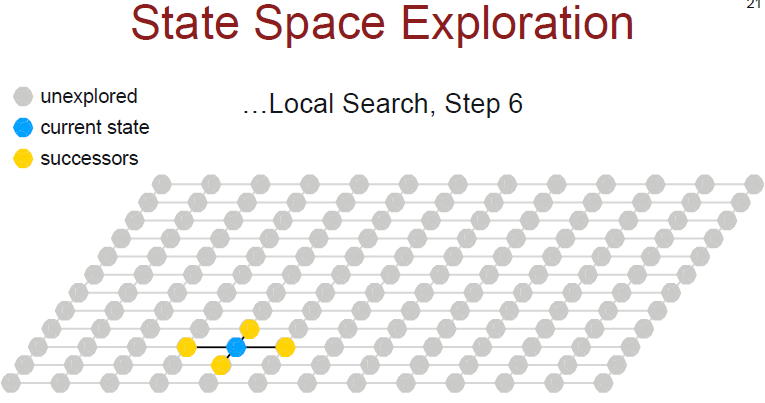
Local Search
• Local search algorithms that keep a single current state, and then try to improve it.
• State space is the set of complete configurations
• In many optimization problems, the path to the goal is irrelevant; the goal state itself is the solution
• We may not know what the goal is! In that case, the search becomes an optimization problem — we return the best state we can find.
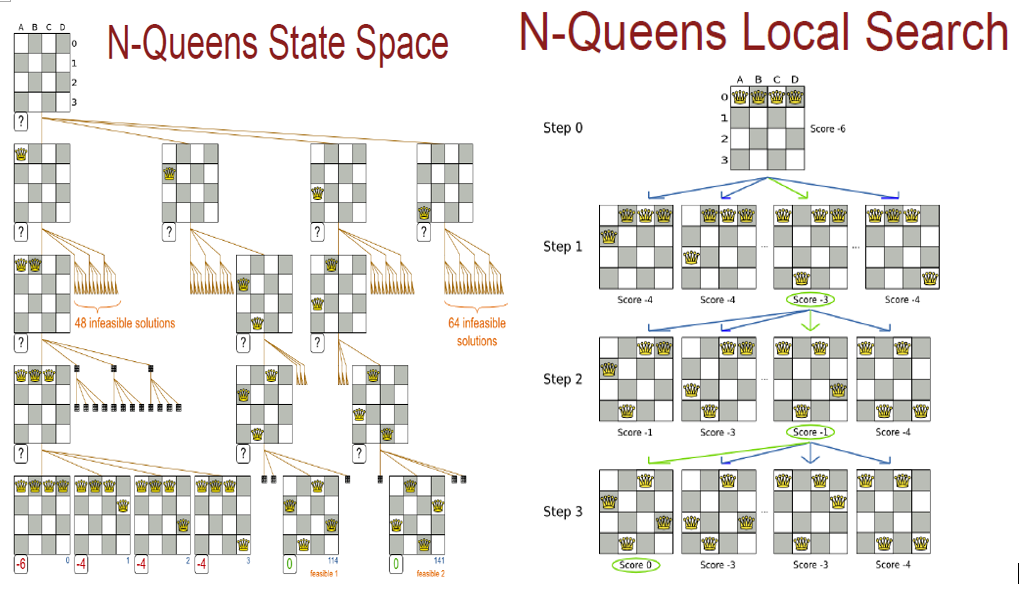
- Hill Climbing Search
1 2 3 4 5 6 7 8 | current_node = INITIAL_STATE while not is_goal(current_node): successors = expand(current_node) best = select_best(successors) if objective(current_node) > objective(best): return current_node else: current_node = best | cs |
= 8-Puzzle Hill Climbing
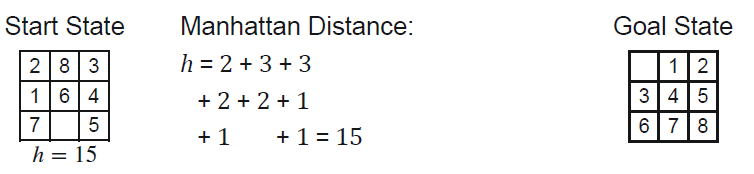
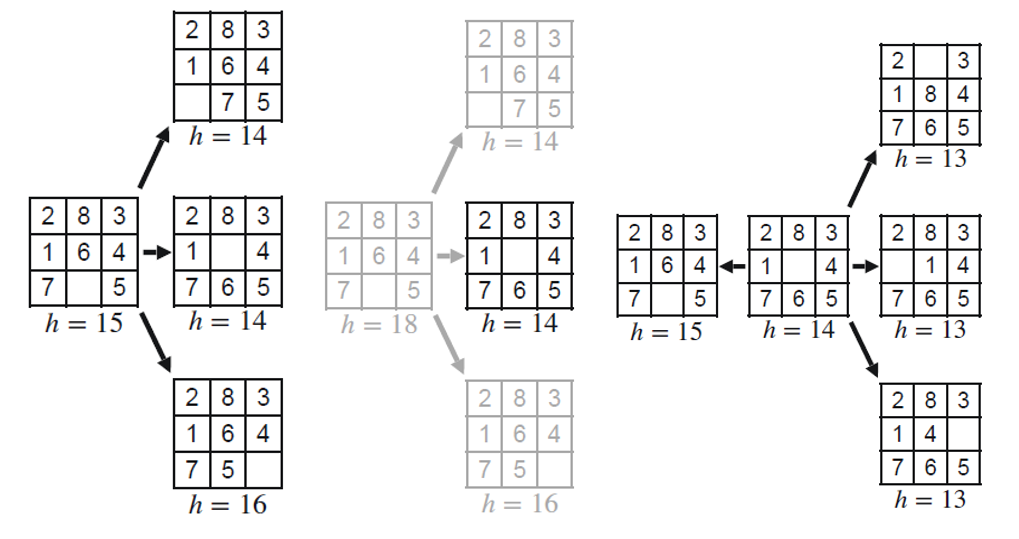
Challenges for Hill Climbing
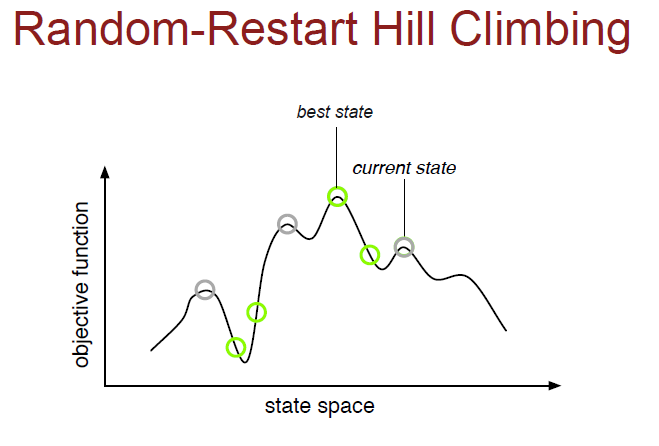
• Local Maxima/Minima – every move has a worse result than the current state. Once a local maximum is reached, there is no way to backtrack or move out of that maximum.
• “Shoulders/Plateaux” – there are no better moves, but some are just as good. Do we keep exploring? Hill climbing can have difficult time finding its way off of a flat portion of the objective function landscape.
So why use local search?
• Low memory requirements – usually constant
• Effective – Can often find good solutions in extremely large state spaces
• Can be useful for optimization problems with continuous, infinite branching factors
• Randomized variants of hill climbing can mitigate many of the drawbacks in practice
Reference: Matthew Hale Rattigan




