Algorithms - Graph, BFS, DFS

- Graph
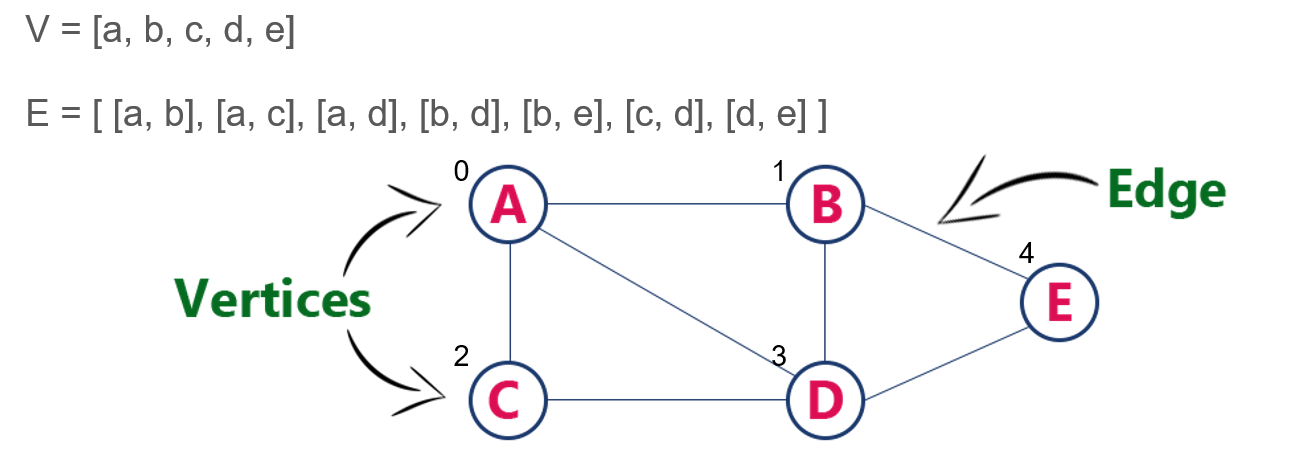
A graph is a pictorial representation of a set of objects where some pairs of objects are connected by links. The interconnected objects are represented by points termed as vertices, and the links that connect the vertices are called edges.
Graphs are used to represent networks. The networks may include paths in a city or telephone network or circuit network. Graphs are also used in social networks like linkedIn, Facebook. Each person is a node that consists of the individuals metadata and the edges are friendships.
-
A graph is a mathematical representation of a network
- Set of nodes (vertices) V
- Set of pairs of nodes (edges) E (a relation)
- Graph G = (V,E)
- Notation: n = |V |, m = |E| (almost always used)
-
Definitions: Edge, Path
-
Edge e = {u, v} — but usually written e = (u, v) u and v are neighbors, adjacent, endpoints of e, e is incident to u and v.
-
A path is a sequence P = v1, v2, . . . , vk−1, vk such that each consecutive pair vi, vi+1 is joined by an edge in G.
Called: path “from v1 to vk”. Or: a v1–vk path.
Special case: empty path from any v to itself (just node, no edges).
-
-
Simple path: path where all vertices are distinct
- Exercise. Prove: If there is a path from u to v then there is a simple path from u to v.
- Different terms elsewhere: walk: arbitrary (called path here), trail: no repeated edges, path (here: simple path)
-
Distance from u to v: minimum number of edges in a u–v path
-
(Simple) Cycle: path v1, . . . , vk−1, vk where
- v1 = vk
- First k − 1 nodes distinct
- All edges distinct
-
Connected component: maximal subset of nodes such that a path exists between each pair in the set.
- maximal = if a new node is added to the set, there will no longer be a path between each pair
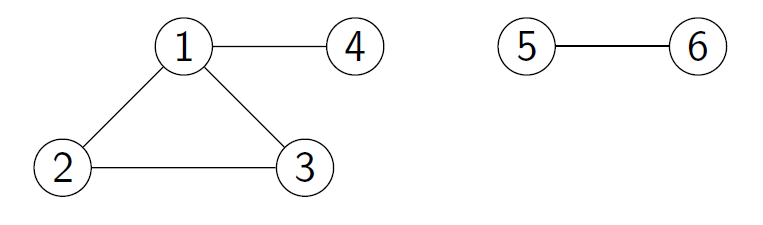
Node set: {1, 2, 4}: there is a path between any two nodes. But it is not maximal: can add 3, property still holds. {1, 2, 3, 4} is maximal: can’t add any other node
- maximal = if a new node is added to the set, there will no longer be a path between each pair
- Trees
Tree = a connected graph with no cycles
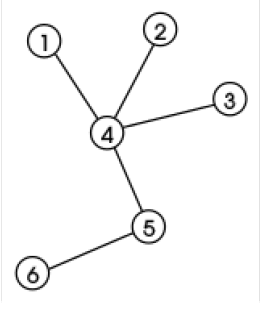
- Tree properties
Let G be an undirected graph with n nodes. Then any two of the following statements imply the third:- G is connected
- G does not contain a cycle
- G has n − 1 edges
- Rooted tree: tree with parent-child relationship
- Pick root r and “orient” all edges away from root
- Parent of v = predecessor on path from r to v
- Directed graph G = (V,E)
- Directed edge e = (u, v) is now an ordered pair
- e leaves u (source) and enters v (sink)
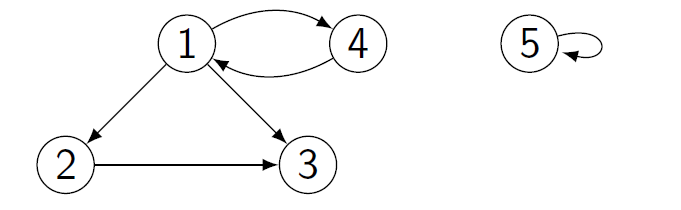
- Directed path, cycle: same as before, but with directed edges
- Strongly connected: directed graph with directed path
between every pair of vertices - Note: graphs undirected if not otherwise specified
- Breadth-First Search (BFS)
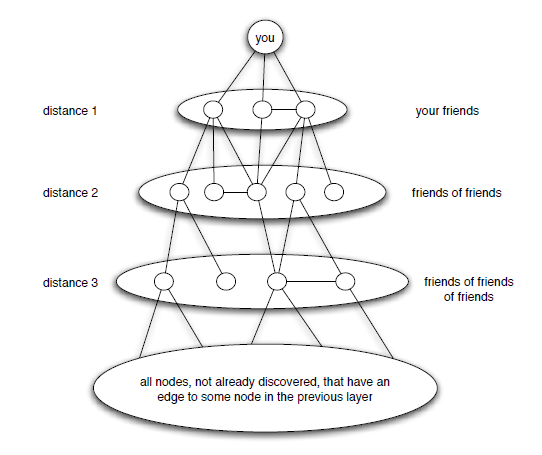
- Explore outward from starting node s.
- Define layer Li = all nodes at distance exactly i from s.
- Layers
- L0 = {s}
- L1 = nodes with edge to L0
- L2 = nodes with an edge to L1 that don’t belong to L0 or L1
- . . .
- Li+1 = nodes with an edge to Li that don’t belong to any earlier layer.
- Observation: There is a path from s to t if and only if t appears in some layer.
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 | BFS(s): mark s as "discovered" 1 L[0] ← {s}, i ← 0 1 # Discover s while L[i] is not empty do L[i + 1] ← empty list <= n for all nodes v in L[i] do n for all neighbors w of v do 2m # Explore v if w is not marked "discovered" 2m then mark w as "discovered" n # Discover w put w in L[i + 1] n end if end for end for i ← i + 1 <= n end while | cs |
Running time: O(m + n). More precisely: Θ(m + n) (why?)
Assumption: can efficiently iterate over neighbors of v. OK with adjacency list.
How to explore entire graph even if it is disconnected?
Running time? Does it change? No, still O(m + n)
Naive: O(m + n) per component ⇒ O(c(m + n)) if c components.
Better: Search on component C only works on nodes/edges in C
- Time for component C: O(#edges in C + #nodes in C)
- O(n) to detect all components (why? how many tests for “unexplored node”?)
- Total time: O(m + n)
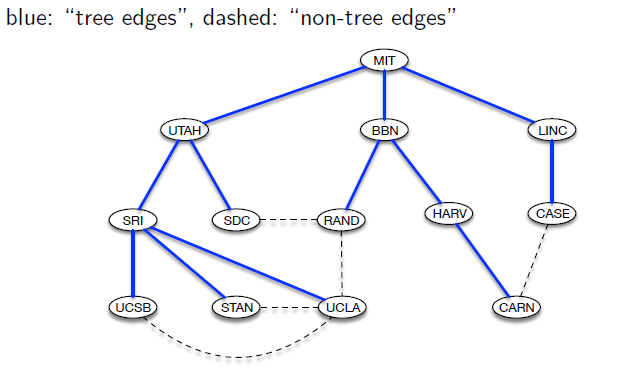
- BFS Tree
Any graph search builds a spanning tree (per connected component)
Tree edges = edges that reach a node for the first time.
1 2 3 4 5 6 7 8 9 10 11 12 13 | BFS(s): mark s as "discovered" L[0] ← {s}, i ← 0 T ← empty # Tree while L[i] is not empty do L[i + 1] ← empty list for all nodes v in L[i] do for all neighbors w of v do if w is not marked "discovered" then mark w as "discovered" put w in L[i + 1] put (v,w) in T # Tree i ← i + 1 | cs |
-
Claim: let T be the tree discovered by BFS on graph G = (V,E), and let (x, y) be any edge of G. Then the layer of x and y in T differ by at most 1.
-
Proof
- Let (x, y) be an edge
- Assume x is discovered first and placed in Li
- Then y ∈ Lj for j ≥ i
- When neighbors of x are explored, y is either already in Li, or is discovered and added to Li+1
- Can we use BFS to detect cycles ?
What if we find a neighbor that’s already discovered?
Cycle! but only if it is not the parent (same edge backwards)
1 2 3 4 5 6 7 8 | for all nodes v in L[i] do for all neighbors w of v do if w is not marked "discovered" then mark w as "discovered" put w in L[i] parent[w] = v # store parent of each node else if w ̸= parent[v] then output "graph has cycle" | cs |
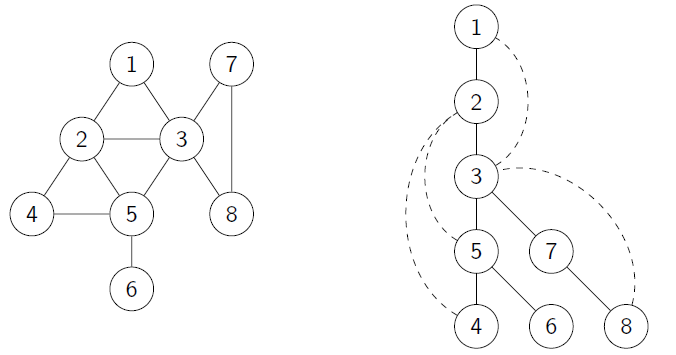
- Depth-First Search (DFS)
Depth-first search (DFS): keep exploring from the most recently added node until you have to backtrack.
- DFS: Recursive Implementation
How to analyze if algorithm is recursive?
Same: count executions of each line, including recursive call
1 2 3 4 5 | DFS(u) mark u as "explored" n for all edges (u, v) do 2m if v is not "explored" then 2m call DFS(v) recursively n | cs |
Running time: O(m + n) same complexity as BFS
Same assumptions: can traverse neighbor list in time proportional to
node degree
- DFS Tree
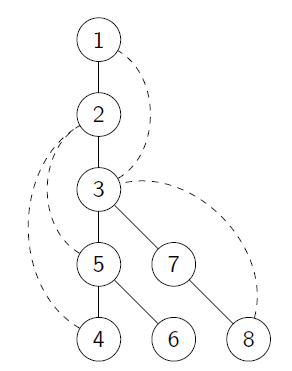
1 2 3 4 5 6 7 | T ← empty DFS(u) mark u as "explored" for all edges (u, v) do if v is not "explored" then put (u, v) in T call DFS(v) recursively | cs |
Claim: Non-tree edges lead to (indirect) ancestors
- Claim: Let T be the tree discovered by DFS, and let (x, y) be an edge of G that is not in T. Then x or y is an ancestor of the other.
- Proof:
All nodes marked explored between call to and return from DFS(v)
are descendents of v. (due to workings of recursion/call stack)- Let x be the first of the two nodes explored
- Is y explored at beginning of DFS(x)? No.
- At some point during DFS(x), we examine the edge (x, y). Is y explored then? Yes, otherwise we would put (x, y) in T
- ⇒ y was explored during DFS(x) ⇒ is a descendant of x
We first see the edge as (y, x) when exploring y: ancestor x is already marked explored, so (y, x) is a back edge.
x can’t be parent of y, since then (x, y) is a tree edge.
- Traversal Implementations
Generic approach:
maintain set of explored nodes and discovered nodes
- Explored = have seen this node and explored its outgoing edges
- Discovered = the “frontier”.
Have seen the node, but not explored its outgoing edges.
Let A = data structure of discovered nodes
1 2 3 4 5 6 7 8 | Traverse(s) put s in A while A is not empty do take a node v from A if v is not marked "explored" then mark v "explored" for each edge (v,w) incident to v do put w in A # w is discovered | cs |
BFS: A is a queue (FIFO) / DFS: A is a stack (LIFO)
Can a node be discovered (placed in A) multiple times? Yes.
For DFS, node is explored from parent that added it last (LIFO).
For BFS, can avoid by not adding discovered nodes.
How to explore entire graph even if it is disconnected?
1 2 3 | while there is some unexplored node s do Traverse(s) # Run BFS/DFS starting from s. Extract connected component containing s | cs |




