Search Engines - Indexing and Ranking/Retrieval

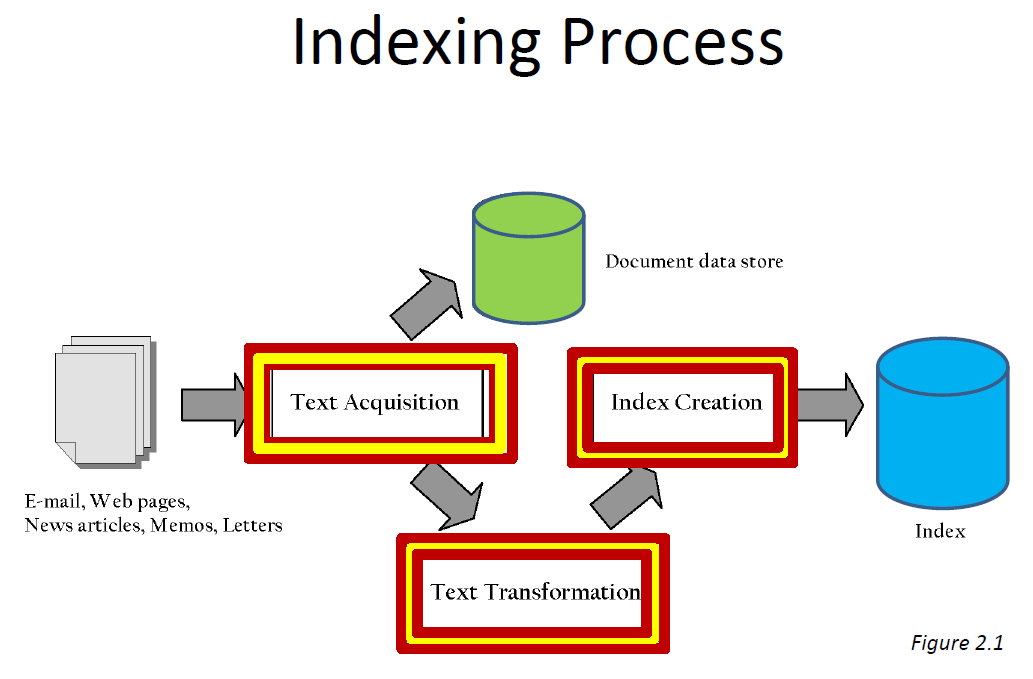
Indexing

• Indexes are data structures designed to make search faster
• Text search has unique requirements, which leads to unique data structures
• Most common data structure is inverted index
  – general name for a class of structures
  – “inverted” because documents are associated with words, rather than words with documents

Indexes and Ranking

• Indexes are designed to support search
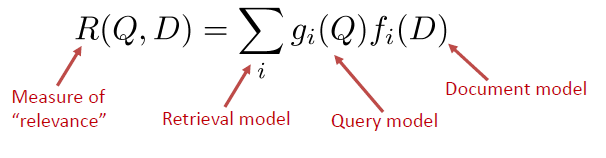
  – faster response time, support updates
• Text search engines use a particular form of search: ranking
  – documents are retrieved in sorted order according to a score computing using the document representation, the query, and a ranking algorithm
• Let’s develop an abstract model for ranking
  – enables discussion of indexes without details of retrieval model
  

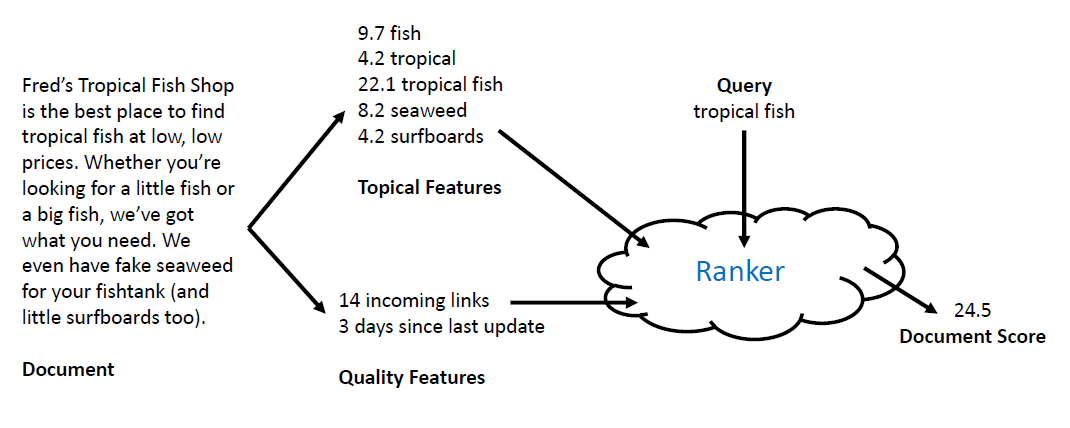
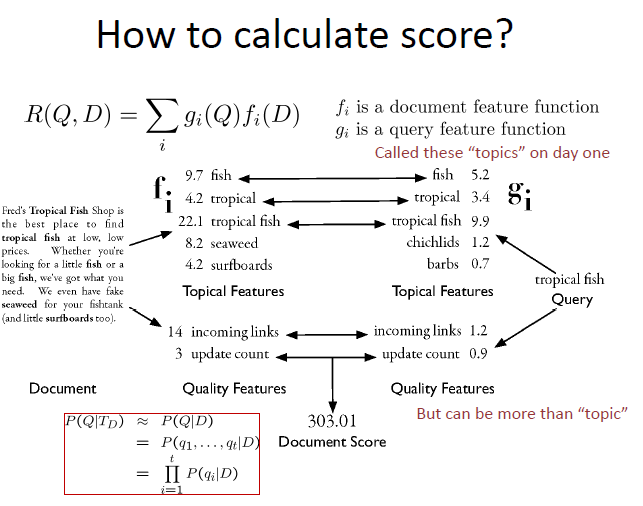
How do we implement ranking?

• Brute force approach
  For each document D in collection: Calculate score and then, Sort the scores
• Drawbacks?
  – Most documents contain no query terms
  – Very slow for a large collection

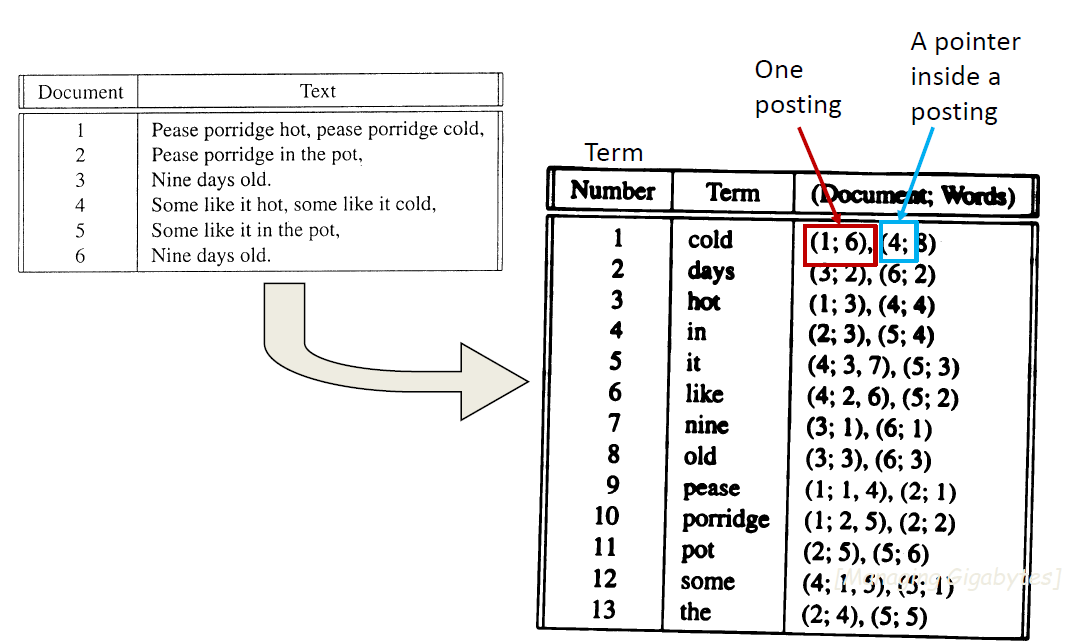
Handle with an inverted Index

• Each term associated with an inverted list
  – Contains lists of documents, or lists of word occurrences in documents, and other information
  – Each entry is called a posting
  – The part of the posting that refers to a specific document or location is called a pointer
  – Each document in the collection is given a unique number
  – Lists usually document-ordered (sorted by document number)

Query Processing

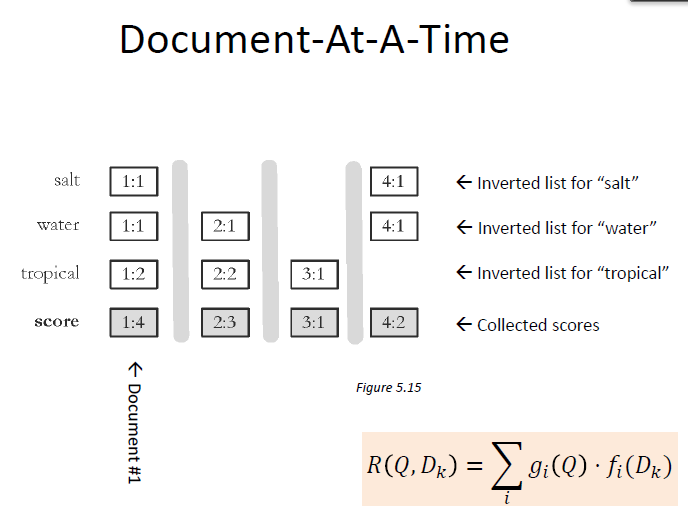
• Document-at-a-time
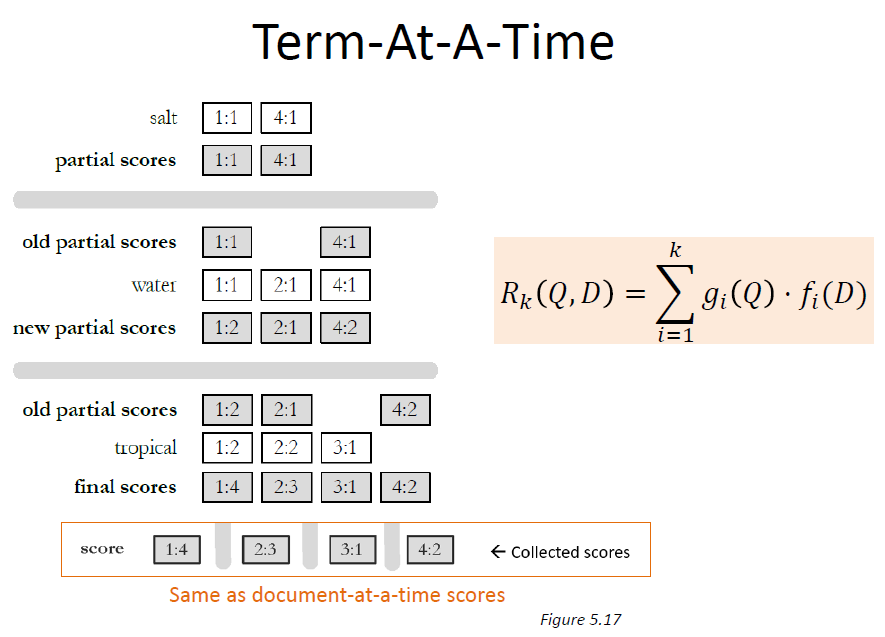
  – Calculates complete scores for documents by processing all term lists, one document at a time
• Term-at-a-time
  – Accumulates scores for documents by processing term lists one at a time
• Both approaches have optimization techniques that significantly reduce time required to generate scores

Pseudocode Function Descriptions

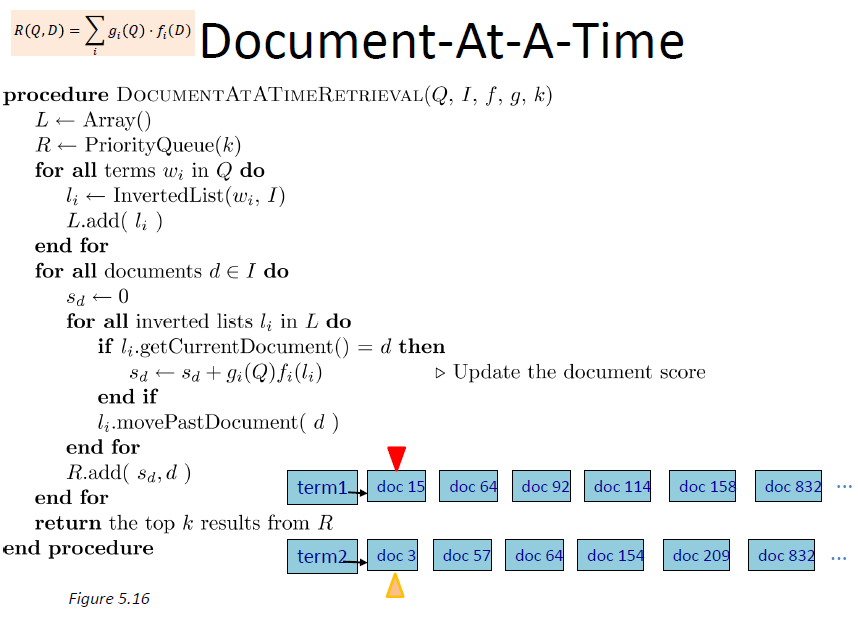
• Need to be able to traverse inverted lists
  – Recall that they are sorted by document number
• Abstraction is a “you are here” pointer
• InvList.getCurrentDocument()
  – Returns the document number of the current posting of the inverted list (“you are here”)
• InvList.movePastDocument(d)
  – Moves forward in the inverted list until getCurrentDocument() > d

Pseudocode Function Descriptions

• getCurrentDocument()
  – Returns the document number of the current posting of the inverted list.
• movePastDocument(d)
  – Moves forward in the inverted list until getCurrentDocument() <= d.
• moveToNextDocument()
  – Moves to the next document in the list. Same as movePastDocument(getCurrentDocument()).

Ranking/Retrieval

Retrieval Models

• Provide a mathematical framework for defining the search process
  – includes explanation of assumptions
  – basis of the ranking algorithms
• Progress in retrieval models has corresponded with improvements in effectiveness
• Theories about relevance

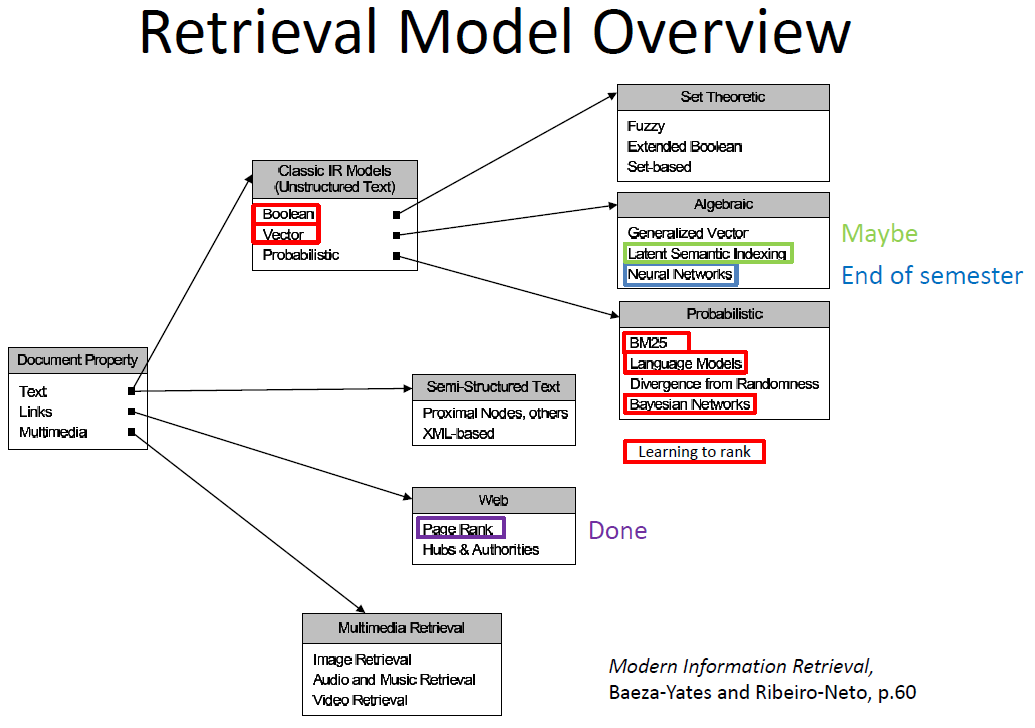
Boolean Retrieval

• Two possible outcomes for query processing
  – TRUE and FALSE
  – “exact-match” retrieval
  – simplest form of ranking
• Query usually specified using Boolean operators
  – AND, OR, NOT
  – proximity operators and wildcards also used
  – Extra features like date or type

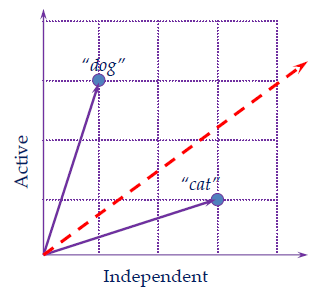
Vector Space Model

• Key idea is that everything is a vector
  – In an extremely high-dimensional space
  – e.g., 100K dimensions
  – documents, queries, terms

• Dimensions are not specified

• Magnitude on them is not specified

• Typically, a document is the sum of its parts

• Provides a framework
  – Dimensions most commonly are terms (tokens)
  – Term weighting for magnitude -> Which terms are more important?
  – So weighted vectors are doc and query models
  – How to rank? -> Which documents are more relevant?
  – Relevance Feedback -> How to employ feedback from searcher?

• Documents and query represented by a vector of term weights

• Collection represented by a matrix of term weights
  

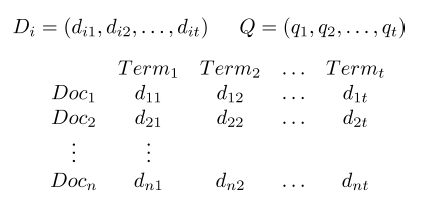
How do we weigh doc terms?

• Is just the number of times it occurs enough?
• Intuition:
  – Terms that appear often in a document should get high weights
  – Terms that appear in many documents should get low weights
• How do we capture this mathematically?
  – Term frequency
  – Inverse document frequency

Term frequency tf

• The term frequency tfd,t of term t in document d is defined as the number of times that t occurs in d.
• We want to use tf when computing query-document match scores. But how?
• Raw term frequency is not what we want:
  – A document with 10 occurrences of the term is more relevant than a document with 1 occurrence of the term.
  – But not 10 times more relevant.
• Relevance does not increase proportionally with term frequency.

Log-frequency weighting

• The log frequency weight of term t in d is
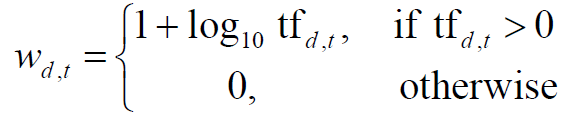
• 0 → 0, 1 → 1, 2 → 1.3, 10 → 2, 1000 → 4, etc.
• Score for a document-query pair: sum over terms t in both q and d:
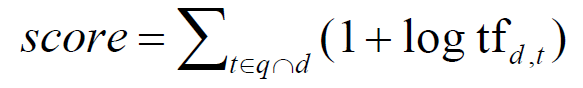
• Score is 0 if none of the query terms is in the document – i.e., if intersection is empty

idf weight

• nk is the document frequency of term k: the number of documents that contain k
  – nk is an inverse measure of the “informativeness” ofa term that occurs k times
  – nk <= N
• We define the idf (inverse document frequency) of k by: idfk = log10 (N/nk )
  – We use log (N/nk) instead of N/nk to “dampen” the effect of idf.
  – A term that occurs zero times has an undefined idf

Term Weights

• tf·idf weight
  – Term frequency weight measures importance in document
  – Inverse document frequency measures importance in collection
  – Heuristic combination (length normalized)
  

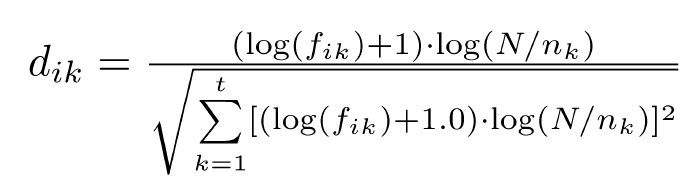
BM25

• BM25 was created as the result of a series of experiments on variations of the probabilistic model
• A good term weighting is based on three principles
  – inverse document frequency
  – term frequency
  – document length normalization
• The classic probabilistic model (just talked about) covers only the first of these principles
• This reasoning led to a series of experiments which led to the BM25 ranking formula
• Popular and effective ranking algorithm based on binary independence model
  – adds document and query term weights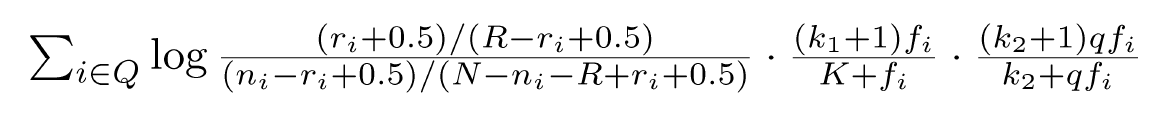
  – k1, k2 and K are parameters whose values are set empirically
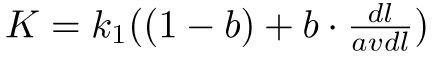  – dl is doc length
  – Typical TREC values: k1 is 1.2, k2 varies from 0 to 1000, b = 0.75

BM25 Example

• Query with two terms, “president lincoln”, (qf = 1)
• No relevance information (ri and R are zero)
• N = 500,000 documents
• “president” occurs in 40,000 documents (n1 = 40, 000)
• “lincoln” occurs in 300 documents (n2 = 300)
• “president” occurs 15 times in doc (f1 = 15)
• “lincoln” occurs 25 times (f2 = 25)
• document length is 90% of the average length (dl/avdl = .9)
• k1 = 1.2, b = 0.75, and k2 = 100
• K = 1.2 · (0.25 + 0.75 · 0.9) = 1.11
  

Query-Likelihood Model (QL)

• Rank documents by the probability that the query could be generated by the document model (i.e., same topic)
• Given a query, we are interested in P(D|Q)
• One way is to use Bayes’ Rule
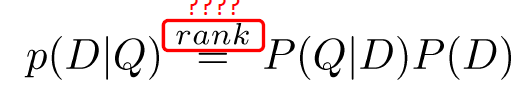
• Assuming prior is uniform, and assuming independence, we get the unigram
  

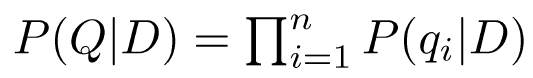
Smoothing

• Document texts are a sample from the language model
  – Missing words should not have zero probability of occurring
  – A document is a very small sample of words, and the maximum likelihood estimate will be inaccurate.
• Smoothing is a technique for estimating probabilities for missing (or unseen) words
  – reduce (or discount) the probability estimates for words that are seen in the document text
  – assign that “left-over” probability to the estimates for the words that are not seen in the text

Query Likelihood Example

• For the term “president”
  – fqi,D = 15, cqi = 160,000
• For the term “lincoln”
  – fqi,D = 25, cqi = 2,400
• number of word occurrences in the document, |D|, is assumed to be 1,800
• number of word occurrences in the collection is 109
  – 500,000 documents times an average of 2,000 words
• Score using JM smoothing with λ=0.1 ?
• Score using Dirichlet smoothing with μ = 2,000?
• Using natural log (doesn’t really matter)
• Query Likelihood Example (Dirichlet)

GitHub - IlMinCho/SE-Indexing

Contribute to IlMinCho/SE-Indexing development by creating an account on GitHub.

GitHubIlMinCho

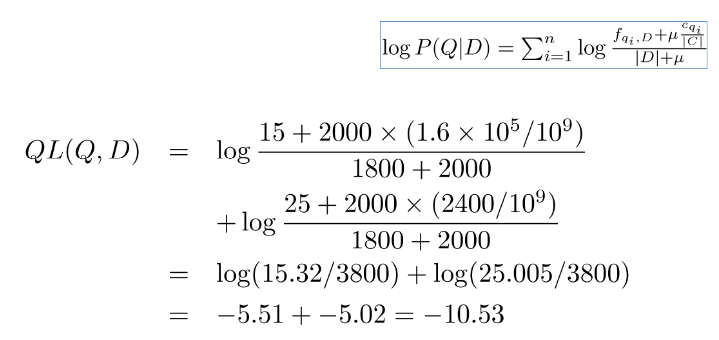
Analysis

1. What is the average length of a story in this collection? What is the shortest story (and how short it is)? What is the longest story (and how longis it)? Note that for this project, "short" and "long" are measured by the number of tokens, not the number of characters.
   Average length = 1215.1629098360656 / 19406-art53 = 4 / 8951-id_6 = 26139
2. What word occurs in the most stories and how many stories does it occur in? What word has the largest number of occurrences and how many does it have?
   ‘the’: 966 docs / ‘the’: 96151 times
3. How many unique words are there in this collection? How many of them occur only once? What percent is that? Is that what you would expect? Why or why not?
   27217 unique terms, 10056 only once. It is around 37%. It is difficult for me to predict the exact value, but it can be calculated to some extent using zipf'law and the larger the size of the corpus and the more diverse the types, the higher the rate of unique words that appear only once, so our sample has a moderate amount of sample and diversity, so 37% is a reasonable number.
4. Your training queries have two queries that are roughly about the scientific american supplement. Suppose that you wanted to judge stories for relevance using a pooling strategy that takes the top 100 documents from each of those two queries. How many unique documents will you be judging? What if you only considered the top 20? Suppose you had a budget that allowed you to judge at most 25 documents. How deeply could you go into the two queries for judging to get 25 judged, no more, no less?
   58 unique documents on top 100 docs. / 0 unique documents on top 20.
   To get 25 unique documents, go in to 64 ranking
5. Run the query amherst college – where that means the two words separately and not the phrase – using either BM25 or QL (your choice). For any 10 of the top 50 top ranked documents, look at the text of the document and mark whether it is relevant. Put your judgments in a file called amherst-YOURUSERNAME.qrels Your should include the 10 storyIDs and a judgement of relevant that is 0 = has nothing to do with Amherst College, 1 = Amherst College is mentioned, or 2 = substantially relates to someone from or
   something that happened at Amherst College. Use the qrels file format from P2, with the queryname being "amherst", then the skip value of 0, then the storyID (NOT your internal docid), and then the 0/1/2 judgment, one of those per line.

Reference: Prof. James Allan